Ermöglicht die Bewohnbarkeit des Mars mit Silica-Aerogel über den Festkörper-Treibhauseffekt

Zu meinen Favoriten hinzufügen

Automatische Übersetzung anzeigen

#Bauausführungen

{{{sourceTextContent.title}}}

{{{sourceTextContent.subTitle}}}

{{{sourceTextContent.description}}}

Es wurden mehrere Ideen vorgelegt, um die Marsoberfläche bewohnbarer zu machen5,6,7,8, aber sie alle beinhalten massive Umweltveränderungen, die in absehbarer Zeit weit über die menschlichen Fähigkeiten hinausgehen werden9. Hier stellen wir einen neuen Ansatz für dieses Problem vor. Wir zeigen, dass weite Teile der Marsoberfläche in Zukunft durch ein Festkörper-Analogon zum atmosphärischen Treibhauseffekt der Erde für photosynthetisches Leben bewohnbar gemacht werden könnten. Konkret demonstrieren wir durch Experimente und Modellierung, dass eine 2-3 cm dicke Schicht Silica-Aerogel unter marsianischen Umweltbedingungen gleichzeitig genügend sichtbares Licht für die Photosynthese durchlässt, gefährliche ultraviolette Strahlung blockiert und die Temperaturen darunter dauerhaft auf über den Schmelzpunkt des Wassers erhöht, ohne dass eine interne Wärmequelle erforderlich ist. Die Platzierung von Siliziumdioxid-Aerogel-Schilden über ausreichend eisreichen Bereichen der Marsoberfläche könnte es daher ermöglichen, dass photosynthetisches Leben dort mit minimalem späteren Eingriff überleben kann. Dieser regionale Ansatz, um den Mars bewohnbar zu machen, ist viel besser zu erreichen als die globale Veränderung der Atmosphäre. Darüber hinaus kann es systematisch und ressourcenschonend entwickelt und heute unter extremen Bedingungen auf der Erde weiter getestet werden.

Um 50 K herum ist auf dem Mars eine Erwärmung der Oberfläche erforderlich, um die jährlichen durchschnittlichen niedrigen bis mittleren Breitentemperaturen auf über den Schmelzpunkt des flüssigen Wassers anzuheben. Die aktuelle Mars-Atmosphäre ist zu dünn, um Ultraviolett (UV) signifikant abzuschwächen oder eine Treibhauserwärmung von mehr als ein paar Kelvin zu erreichen. Beobachtungen von dunklen Flecken auf den polaren Kohlendioxid-Eiskappen des Mars deuten jedoch darauf hin, dass sie vorübergehend um eine größere Menge über ein planetarisches Phänomen erwärmt werden, das als Festkörper-Treibhauseffekt10,11,12,13 bekannt ist, der entsteht, wenn Sonnenlicht im Inneren von transparenten Schnee- oder Eisschichten absorbiert wird14,15. Der Festkörper-Treibhauseffekt ist am stärksten bei Materialien, die für sichtbare Strahlung teilweise transparent sind, aber eine niedrige Wärmeleitfähigkeit und einen niedrigen Infrarot-Durchlässigkeitsgrad aufweisen (Abb. 1). Obwohl Kohlendioxid und Wassereis auf dem Mars verbreitet sind, sind sie viel zu flüchtig, um robuste Solid-State-Treibhausschilde für das Leben zu schaffen. Kieselsäure hat günstigere Eigenschaften, da sie chemisch stabil und feuerfest bei marsianischen Oberflächentemperaturen ist. Feste Kieselsäure ist für sichtbare Strahlung transparent, aber undurchsichtig für UV bei Wellenlängen kürzer als 200-400 nm und für Infrarot bei Wellenlängen länger als ~2 μm, abhängig von der Fülle von Verunreinigungen wie Hydroxygruppen. Die Wärmeleitfähigkeit von festem Siliziumdioxid (0,8-1,6 W m-1 K-1) (Ref. 16) ist jedoch zu hoch, um eine starke Erwärmung zu ermöglichen.

Silica-Aerogele, die aus nanoskaligen Netzwerken von miteinander verbundenen Silica-Clustern bestehen, sind zu über 97 Vol.-% Luft und haben einige der niedrigsten gemessenen Wärmeleitfähigkeiten eines bekannten Materials (~0,02 W m-1 K-1 bei 1 bar Druck oder 0,01 W m-1 K-1 bei Marsatmosphärendruck)17. Aufgrund dieser Eigenschaften haben Silica-Aerogele in vielen Bereichen der Technik an Bedeutung gewonnen, darunter auch bei der Konstruktion passiv beheizter Gebäude auf der Erde18 und sogar bei den Mars Exploration Rovers, wo dünne Aerogelschichten zur Wärmedämmung bei Nacht eingesetzt wurden19. Silica-Aerogelen haben daher ein ausgezeichnetes Potenzial für eine starke Erwärmung des Festkörper-Treibhauses unter maritimen Bedingungen.

Wir führten Experimente durch, um das Erwärmungspotential von Siliziumdioxid-Aerogel-Halbleiter-Treibhausschichten unter marsähnlichen Sonneneinstrahlungswerten zu demonstrieren. Unser Versuchsaufbau besteht aus einer Schicht von Siliziumdioxid-Aerogel-Partikeln oder -Fliesen (siehe Abb. 2) auf einer Basis mit niedriger Reflexionsfähigkeit, die von einem wärmeisolierenden Material umgeben ist (siehe Methoden). Das Gerät wird der sichtbaren Strahlung eines Sonnensimulators ausgesetzt. Der auf die Schicht einfallende breitbandige Fluss wird mit einem Pyranometer gemessen, und die Temperatur wird durch kalibrierte Glasperlenthermistoren aufgezeichnet.

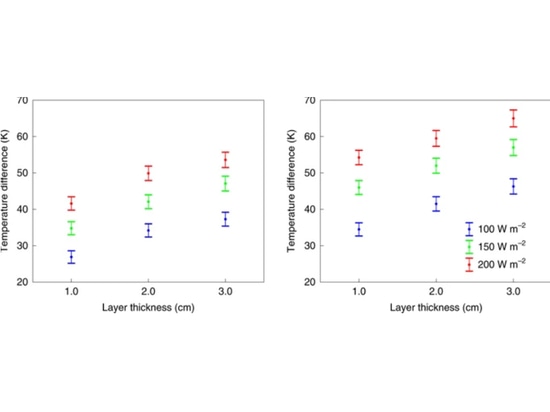
Abbildung 3 zeigt die experimentellen Ergebnisse sowohl für Aerogelpartikel- als auch für Fliesenschichten im Vergleich zum empfangenen sichtbaren Fluss im Bereich von 100-200 W m-2. Zum Vergleich: Der globale mittlere empfangene Fluss der Erde ist 342 W m-2, während der des Mars 147 W m-2 ist. Wie man sehen kann, werden Temperaturunterschiede von über 45 K für Aerogelpartikelschichten mit einer Dicke von 3 cm erreicht, die einen Fluss von 150 W m-2 erhalten. Aerogel-Fliesen, die eine höhere sichtbare Transmission aufweisen, verursachen Temperaturunterschiede, die ~10 K höher sind und bei nur 2 cm Dicke >50 K erreichen. Unsere experimentellen Ergebnisse zeigen, dass unter Mars-ähnlichen Sonneneinstrahlungswerten eine Erwärmung auf den Schmelzpunkt von flüssigem Wasser oder höher unter einer 2-3 cm dicken Silica-Aerogelschicht erreicht werden kann. Die maximal erreichbare Erwärmung ist wahrscheinlich noch höher (siehe Methoden), da in unserem Versuchsaufbau über Seitenwand- und Bodenwärmeverluste und Konvektion Wärme verloren geht. Wir haben auch die Transmission der Aerogelpartikel und -kacheln im UV gemessen und eine starke Dämpfung von UVA und UVB (280-400 nm) und eine nahezu vollständige Dämpfung der gefährlichsten UVC-Strahlung (220-275 nm) festgestellt (Abb. 4).

Obwohl die Erhöhung der Oberflächentemperaturen und die Blockierung der UV-Strahlung die beiden wichtigsten Faktoren für das Überleben auf dem Mars sind, müssen auch zusätzliche Einschränkungen durch Luftdruck, Nährstoffverfügbarkeit und Staubablagerung berücksichtigt werden. Sole kann unterhalb des Gefrierpunktes von reinem Wasser flüssig bleiben, was den Temperaturbedarf unter die hier angenommene 273 K senken könnte20, obwohl bei ausreichender Salinität die Bewohnbarkeit nur auf halophile Organismen beschränkt wäre. Der höhere Kohlendioxidpartialdruck auf dem Mars gegenüber der Erde ist für das Pflanzenwachstum günstig6, aber der niedrige atmosphärische Gesamtdruck bedeutet, dass bei Temperaturen von 273 K oder höher die Unterseiten der Silica-Aerogel-Treibhausschilde in Bezug auf die Atmosphäre leicht unter Druck bleiben müssten, um einen Verlust von Wasserdampf sowohl vertikal als auch seitlich zu vermeiden. Dies würde leichte Anforderungen an ihre strukturellen Eigenschaften stellen, die plausibel erfüllt werden könnten, indem das Silica-Aerogel mit dünnen Schichten aus festem transparentem Material oder mit organischen Polymeren verstärkt21,22 durchsetzt wird. Die meisten Nährstoffe scheinen auf der Marsoberfläche leicht verfügbar zu sein, wobei die Häufigkeit einiger (wie Eisen und Schwefel) höher ist als auf der Erde23. Der niedrige Partialdruck von N2 auf dem Mars kann eine Herausforderung für die Stickstofffixierung durch nicht angepasste terrestrische Mikroorganismen darstellen. Nitratablagerungen, die in situ auf der Marsoberfläche beobachtet wurden, sind jedoch eine plausible alternative Quelle von nitrogen24.

Die günstigsten Standorte auf dem Mars für die Schaffung lokaler lebenserhaltender Regionen sind diejenigen, die die wichtigsten Ressourcen von Licht- und Oberflächenwasser kombinieren und gleichzeitig Gefahren wie übermäßige Staubablagerungen minimieren. Innerhalb des Breitenbereichs, in dem der Sonnenfluss das ganze Jahr über hoch ist (45° S-45° N), gibt es viele Standorte in der Mitte der Breite, an denen Beobachtungen darauf hindeuten, dass oberflächennahes Bodeneis vorhanden ist25,26,27 und Klimamodellsimulationen28 darauf hindeuten, dass die Staubansammlungsraten niedrig sein sollten. Abbildung 4 zeigt die Ergebnisse einer gekoppelten strahlungsthermischen Berechnung für die Entwicklung der marsianischen Untergrundtemperaturen an einer solchen Stelle (Deuteronilus Mensae) in Gegenwart einer Festkörper-Treibhaus-Siliziumdioxid-Aerogelschicht. Unser Modell berücksichtigt Veränderungen der Marsisolation und des aerogelischen Strahlungsübergangs, die Wärmeleitung sowohl im Aerogel als auch im Regolithen und die mit dem Schmelzen/Gefrieren von Regolitheis verbundene latente Wärme (siehe Methoden). Wie in Abb. 5 zu sehen ist, sind bei Vorhandensein einer 2.5 cm dicken Aerogelschicht die Untergrundtemperaturen bis in Tiefen von mehreren Metern hoch genug, um nach einigen Jahren an dieser Stelle flüssiges Wasser während des gesamten Marsjahres zuzulassen.

Unsere Ergebnisse zeigen, dass durch den Festkörper-Treibhauseffekt Regionen auf der Marsoberfläche in Zukunft so verändert werden könnten, dass Leben dort mit viel weniger Infrastruktur oder Wartung überleben kann als durch andere Ansätze. Die Schaffung dauerhaft warmer Regionen hätte viele Vorteile für die zukünftige menschliche Aktivität auf dem Mars, ist aber auch von grundlegendem Interesse für astrobiologische Experimente und als potenzielles Mittel zur Erleichterung der Bemühungen zur Lebenserkennung29. Das Festkörper-Treibhaus-Wärmekonzept hat auch Anwendungen für die Forschung in feindlichen Umgebungen auf der Erde, wie der Antarktis und der chilenischen Atacama-Wüste.

In zukünftigen Arbeiten wird es wichtig sein, zu untersuchen, mit welcher Leichtigkeit traditionelle Techniken zur Herstellung von Silica-Aerogelen17 an die Bedingungen auf dem Mars angepasst werden können. Angesichts der Fähigkeit des Lebens auf der Erde, seine Umwelt zu verändern, ist es jedoch auch interessant zu prüfen, inwieweit Organismen letztendlich dazu beitragen könnten, die Lebensbedingungen des Mars selbst zu erhalten. Auf der Erde gibt es bereits mehrere Organismen, die Siliziumdioxid als Baumaterial verwenden, darunter Hexactinellidschwämme und Kieselalgen-Phytoplankton30,31. Insbesondere Diatomeen können bis zu mehreren Millimetern lang werden, produzieren Sturzpartikel aus amorphen Siliziumdioxidpartikeln mit ~1-10 nm Durchmesser (kleiner als der mittlere Porendurchmesser in Siliziumdioxid-Aerogel-Netzwerken)17,32 und haben bereits ein hohes Potenzial für Anwendungen der Bionanotechnologie in anderen Bereichen31,33. Daher könnte es in Zukunft interessant sein zu untersuchen, ob hochvisuelle Transmissivität und niedrige Wärmeleitfähigkeit von Kieselsäure-Schichten direkt über einen synthetisch-biologischen Ansatz hergestellt werden können. Wenn dies möglich ist, könnte es in Kombination mit den hier beschriebenen Ergebnissen schließlich die Entwicklung einer sich selbst tragenden Biosphäre auf dem Mars ermöglichen.

Da es das Potenzial gibt, den Mars kurz- bis mittelfristig für das photosynthetische Leben bewohnbar zu machen, müssen wichtige ethische und philosophische Fragen berücksichtigt werden. Am offensichtlichsten ist, dass, wenn der Mars heute noch über vorhandenes Leben verfügt, sein Überleben oder seine Entdeckung durch das Vorhandensein von Mikroorganismen auf der Erde behindert werden könnte34. Allerdings hat noch keine Mission Leben auf dem Mars entdeckt, so dass sie, wenn sie existiert, wahrscheinlich auf ganz bestimmte Regionen im Untergrund beschränkt sein wird. Der hier untersuchte Ansatz würde nicht zum Überleben des erdbasierten Lebens außerhalb von Festkörper-Gewächshausregionen führen, so dass es unwahrscheinlich sein dürfte, dass die Suche nach maritimem Leben ein größeres Risiko darstellt als die Anwesenheit von Menschen an der Oberfläche. Dennoch sind die Belange des planetarischen Schutzes im Zusammenhang mit der Übertragung von Leben auf der Erde auf den Mars wichtig, weshalb die astrobiologischen Risiken, die mit diesem Ansatz zur Bewohnbarkeit des Mars verbunden sind, sorgfältig gegen den Nutzen für die Mars-Wissenschaft und die menschliche Erforschung in Zukunft abgewogen werden müssen.

Unser Versuchsaufbau bestand aus einer 18 cm × 18 cm Festkörper-Gewächshausschicht variabler Dicke, die zur Isolierung von Polystyrol umgeben war, mit einem Sonnensimulator, der über der Schicht positioniert war, um unterschiedliche Niveaus der sichtbaren Bestrahlungsstärke zu erreichen (Ergänzung Abb. 1). Für die Festkörper-Treibhausschicht verwendeten wir Kombinationen von Silica-Aerogel-Partikeln (Radien zwischen 700 μm und 4 mm; Lumira, Cabot Aerogel) und Fliesen (10 cm × 10 cm × 1 cm; Large Hydrophobic Silica Tiles, Tiem Factory). In den Partikelexperimenten wurde die gesamte Schicht mit Partikeln gefüllt, während in den Fliesenexperimenten die Fliesen in der Mitte platziert und das restliche Volumen mit Partikeln gefüllt wurde. Der flachflorige schwarze Filz aus sichtbarem Albedo <0,01 (Protostar beflocktes Lichtfallenmaterial) wurde unter die Aerogelschicht gelegt, um die Absorption der einfallenden sichtbaren Strahlung aus dem Sonnensimulator zu maximieren.

Die Temperaturdaten wurden über eine Reihe von kompakten (0,8 mm Durchmesser) Negativ-Temperaturkoeffizienten-Thermistoren erfasst. Die Thermistoren wurden mit einem digitalen Referenzthermometer (rückführbares Modell 1235D30) zwischen 0 °C und 100 °C kalibriert, indem sie in einem kontinuierlich gerührten Wasserbad aufgehängt und gleichzeitig der Thermometerwert und der Thermistorwiderstand erfasst wurden. Anschließend wurde mit Hilfe einer Kleinste-Quadrat-Passung der Widerstand in Abhängigkeit von der Temperatur nach der Formel

wobei R der Widerstand in Kilo-Ohm, T die Temperatur in Kelvin, T0 = 273.15 K eine Referenztemperatur und C und β Kalibrierkonstanten sind. Die Kalibrierergebnisse und Best-Fit-Werte für C und β sind in der ergänzenden Abbildung 2 dargestellt. Wir haben auch den Unterschied im Widerstand zwischen einzelnen Thermistoren bei gleicher Temperatur getestet und fanden ihn im Vergleich zu anderen Fehlerquellen im interessierenden Temperaturbereich minimal. Thermistoren wurden an der Basis, der Oberseite und der Außenseite der Solid-State-Gewächshausvorrichtung angebracht und mit einer Spannungsteilerschaltung verbunden, die mit einem Multiplexer/ESP8266-Mikrocontroller zur Datenerfassung verbunden ist. Wir verwendeten auch eine kleine Wärmebildkamera (Seek Thermal Imager) als zusätzliche Überprüfung der von den Thermistoren aufgezeichneten Temperaturdaten und zur Diagnose von Seiten- und Basisbereichen mit erhöhtem Wärmestrom während des Versuchsaufbaus.

Eine sichtbare Beleuchtung zur Simulation des Sonnenstroms wurde durch eine 250 W geschützte Pulsstart-Metallhalogenidlampe bereitgestellt. Eine Metall-Halogenid-Lichtquelle wurde gewählt, weil sie bei den meisten Wellenlängen dem Null-Luft-Masse-Sonnenspektrum (AM0) näher kommt als andere Lichtquellen wie Xenon-Lichtbogen35 bei geringeren Kosten und reduziertem Explosionsrisiko. Die Lampe wurde in einen lüftergekühlten Leuchtkasten mit verspiegelter Decke und schwarzen Seitenwänden eingekapselt, um die Übertragung von gut kollimiertem Licht auf die Aerogelschicht zu maximieren (Ergänzende Abb. 1). Als Vorsichtsmaßnahme gegen den Ausfall einer explosiven Lampe wurde zwischen Lampe und Experiment eine Glasscheibe angebracht. Der Prozentsatz des Sonnenstroms, der oberhalb der Wellenlängen auftritt, bei denen das Glas beginnt, signifikant zu absorbieren (2-3 μm), liegt in der Größenordnung von wenigen Prozent, so dass die Absorption der Nahinfrarotstrahlung durch die Abschirmung nicht als signifikante Fehlerquelle in unseren Ergebnissen angesehen wurde. Die optischen Eigenschaften von Silica-Aerogel variieren nicht signifikant über den sichtbaren Wellenlängenbereich36, so dass die relativ kleinen Unterschiede zwischen dem Metallhalogenidlampenspektrum und dem auf die Marsoberfläche einfallenden Sonnenspektrum auch in unseren Ergebnissen keine wesentliche Unsicherheitsquelle darstellten. Die Lampe wurde zwischen 20 cm und 30 cm über der Silica-Aerogel-Probe positioniert. Eine Laborbuchse wurde verwendet, um die Aerogelschicht und die Pyranometerhöhe anzupassen, um den empfangenen Strahlungsfluss zu variieren. Alle Experimente wurden bis zum Erreichen des thermischen Gleichgewichts durchgeführt, das durch Beobachtung des Wertes und der Änderungsrate der Temperatur an der Basis und Oberseite der Silica-Aerogelschicht beurteilt wurde. Typischerweise dauerte dies ~2 h für jedes Experiment. Die Experimente wurden bei Umgebungsdruck und einer Umgebungstemperatur von 298 ± 1 K durchgeführt.

Die auf die Probe einfallenden breitbandigen sichtbaren Flüsse wurden mit einem erstklassigen Doppelglaskuppelpyranometer (Hukseflux Instruments Modell SR-11) gemessen. Das verwendete SR-11-Modell hatte eine Empfindlichkeit von 14.22 × 10-6 ± 0.15 V pro W m-2 und damit einen Kalibrierungsfehler von ±1%. Die geschätzte stündliche Unsicherheit in äquatorialen Breitengraden bei Feldbeobachtungen, die in der Fachliteratur des Pyranometers angegeben ist, betrug ±3,1%, was der Wert ist, den wir bei der Angabe unserer Flussmessunsicherheiten verwendeten (siehe ergänzende Abb. 3). Die räumliche Variation des einfallenden Flusses wurde aufgezeichnet, indem das Pyranometer über ein 0,15 m × 0.15 m Gitter in 3 cm Intervallen bewegt wurde (Ergänzende Abb. 4). Die zeitliche Variabilität des Flusses wurde ebenfalls gemessen und betrug <2% über ein 2 h Intervall (Ergänzende Abb. 4). Die UV-Durchlässigkeitsexperimente wurden mit einer kompakten 4 W UV-Lampe mit zwei Röhren durchgeführt, um die Strahlung zu emittieren, die entweder im 365 nm (UVA und UVB) oder 254 nm (UVC) Bereich liegt. Für die UV-Messung (siehe Zusatztabelle 1) verwendeten wir kalibrierzertifizierte Sper Scientific UVA-, UVB- und UVC-Detektoren, die eine angegebene Genauigkeit von ±4% hatten. Der UVA- und UVB-Detektor hatte eine Spitzenempfindlichkeit im Bereich von 350-360 nm, mit dem Kalibrierpunkt bei 365 nm, während der UVC-Detektor eine Spitzenempfindlichkeit bei 255-265 nm, mit dem Kalibrierpunkt bei 254 nm hatte.

Für die Temperaturdifferenzmessung wurden Fehler aus vier Quellen berücksichtigt: der Digitalisierungsfehler der Datenerfassung, die Unsicherheit des Spannungsteilerwiderstandes und die Fehler in den Kalibrierparametern C und β. Der Digitalisierungsfehler war 3.3 V/210 = 3.2 mV, bezogen auf das verwendete Zehn-Bit-Datenerfassungssystem, oder 3.2 mV, während der Widerstandsfehler des Spannungsteilers 1% oder 0.1 kΩ für den Widerstand 10 kΩ betrug. Die Fehler in C und β wurden aus der loglinearen Anpassung der kleinsten Quadrate berechnet und sind in der ergänzenden Abb. 2 dargestellt.

wobei V0 = 3.3 V die Spitzenspannung ist, T(Va) die Top-of-Layer-Temperatur ist, T(Vb) die Basistemperatur ist und Vi und R1,i jeweils dem Ausgangsspannungs- und Teilerfestwiderstand für Standort i entsprechen. Wir propagierten Unsicherheiten in Va, R1,a, Vb, R1,b, C und β über eine Taylor-Expansion unter Annahme kleiner Unsicherheiten37. Die daraus resultierenden geschätzten Unsicherheiten in ΔT, die zur Erstellung der Fehlerbalken in Abb. 3 verwendet wurden, sind in der ergänzenden Abb. 5 dargestellt.

Eine idealisierte Obergrenze für die Erwärmung von Festkörper-Gewächshäusern lässt sich ableiten, wenn man ein Material mit Null-Wärmeleitfähigkeit betrachtet, das unterhalb einer Grenzwellenlänge λc vollkommen transparent ist, aber bei längeren Wellenlängen absorbiert. Unter diesen Umständen kann die Kühlung nur durch Strahlung von der Basis der Schicht im Sichtbaren erfolgen, und die Basis-Energiebilanz wird dadurch ausgeglichen

wobei λ die Wellenlänge ist, Bλ[T] die spektrale Planck-Bestrahlungsstärke ist, T die Basistemperatur ist und Fb die sichtbare Strahlung (bei Wellenlängen kürzer als λc) ist, die an der Schichtbasis absorbiert wird. Bei der Standarddefinition für Bλ[T] kann die Gleichung (3) durch einen Wurzelfindungsansatz gelöst werden. Der jährliche globale mittlere Sonnenfluss, der vom Mars empfangen wird, ist ~150 W m-2. Bei λc = 2 μm und Fb = 150 W m-2 ergibt Gleichung (3) T = 721 K, die nahe der Oberflächentemperatur der Venus liegt. Eine Verschiebung von λc auf kleinere Werte würde zu noch höheren T-Werten führen, wobei die Temperatur asymptotisch zur effektiven Schwarzkörpertemperatur des Sonnenspektrums als λc → 0 erreicht wurde.

Realistischerweise können wir die Dicke bestimmen, die für eine Solid-State-Gewächshausschicht erforderlich ist, um die Oberflächentemperatur zu maximieren, wenn ihre optische Extinktionstiefe im Sichtbaren nicht vernachlässigbar ist, wie dies bei allen realen Materialien der Fall ist. Dabei vernachlässigen wir dreidimensionale und basale Leitungseffekte und gehen von einer konstanten Wärmeleitfähigkeit aus. Wir gehen auch davon aus, dass die Festkörper-Gewächshausschicht Infrarot-Strahlung effektiv absorbiert, so dass die Leitfähigkeit die dominierende Art des Wärmetransports in der Schicht ist. Diese Analyse baut auf früheren theoretischen Studien zum Festkörper-Treibhauseffekt in Schnee und Eis auf12,15,38.

Wenn die Festkörper-Gewächshausschicht einen Nicht-Null-Ausstiegskoeffizienten im Sichtbaren aufweist, hängt Fb von h, der Gesamtschichtdicke, ab. Dann hängt die vollständige Erwärmung von einem Gleichgewicht zwischen der Dämpfung der sichtbaren Strahlung und der Wärmedämmung durch die Schicht ab. Aus der Thermodiffusionsgleichung ergibt sich ein stationärer Temperaturgradient innerhalb der Schicht von39

wobei Fa der einfallende Sonnenstrom auf die Schicht ist, τ die optische Tiefe der Schicht ist, α der Extinktionskoeffizient der Schicht im Sichtbaren und μ¯ der mittlere solare Zenitwinkel Cosinus ist, folgt daraus unmittelbar, dass die optische Tiefe für die maximale Erwärmung τm τm/μ¯=1 ist und die optimale Schichthöhe hm ist

Unter der Annahme, dass die Transmissionswerte für vertikale Pfade T=e-τ=0,8 und 0,6 für die 1 cm-dicken Silica-Aerogel-Fliesen/Partikelschichten betragen, finden wir α = 22.3 m-1 und 51.1 m-1, oder hm = 4.5 cm und 2.0 cm, angegeben unter μ¯=1. Letzterer Wert liegt relativ nahe an der Schichttiefe der maximalen Erwärmung im Aerogelpartikelgehäuse (siehe Abb. 3), wobei der geringe Unterschied wahrscheinlich auf mehrere Streueffekte zurückzuführen ist. Nach Gleichung (5) ist die theoretische maximale Temperaturdifferenz einfach nur

Gegeben Fa = 150 W m-2 und κ = 0.02 W m-1 K-1, ΔTm = 124 K für die Fliesen und ΔTm = 54 K für die Partikel. Die in unseren Experimenten erzielten Temperaturunterschiede waren geringer, da wir nur Aerogelschichtdicken von bis zu 3 cm verwendeten und Verluste durch Konvektion sowie Seitenwand- und Bodenleitung in unserem relativ kleinen Gerät nicht vernachlässigbar waren.

Unser numerisches Modell des Festkörper-Treibhauseffekts auf dem Mars berechnet den tagesdurchschnittlichen Strahlungsübergang der Aerogelschicht, den Wärmetransport durch Diffusion im darunter liegenden Regolith und den solaren Zenitwinkel in Abhängigkeit von Zeit und Ort. Die Abwärtsstrahlung der Sonne und die Wärmestrahlung der Marsatmosphäre werden mit Daten aus der Mars Climate Database (MCD) Version 5.3 Climatology Szenario (http://www-mars.lmd.jussieu.fr/mars/access.html)2 berechnet. Das solare Zenitwinkelmodell ähnelt dem in Ref. 40 (siehe auch Ref. 39), wobei die Schräglage, Exzentrizität und der Saisonwinkel des Perihelions der Marsumlaufbahn nach dem in Ref. 41, und der Saisonwinkel, der über Keplers Gleichung42 mit der Zeit verknüpft ist. Unsere Modellleistung wurde unter Standard-Marsianischen Bedingungen validiert, verglichen mit Abbildung 1 von Ref. 43 und im Vergleich zu den MCD-Ergebnissen.

Hier ist z die Tiefe, κr die Regolith-Wärmeleitfähigkeit, ch die Wärmekapazität, ρ die Dichte und q die lokale Erwärmungsrate aufgrund von latenten Wärmeeinflüssen. Wir lösen Gleichung (10) über eine zentrierte Differenz im räumlichen Bereich und ein explizites Vorwärtsschreiten in der Zeit.

Unsere Modelldomäne erstreckt sich von der Oberfläche bis in die Tiefe von 80 m und wir integrieren über einen Zeitraum von 15 Marsjahren (Ergänzende Tabelle 2). Wir vernachlässigen horizontale Wärmeverluste, so dass unser Modell für einen Aufbau geeignet ist, bei dem die horizontale Ausdehnung der Festkörper-Gewächshausschicht in beide Richtungen Dutzende von Metern oder mehr beträgt. Da die Festkörper-Treibhausschicht nur wenige Zentimeter dick ist, gehen wir davon aus, dass sie sich zu jedem Zeitpunkt im thermischen Gleichgewicht befindet. Das thermische Gleichgewicht am oberen Ende der Schicht gilt als

wobei FIR die Abwärtswärmestrahlung aus der Marsatmosphäre (geliefert vom MCD) ist, Tb die Temperatur unmittelbar unter der Schicht ist und κ und h wie in Gleichung (4) definiert sind. Dieser Ansatz vernachlässigt eine zusätzliche Erwärmung oder Kühlung der Oberfläche durch sensible oder latente atmosphärische Effekte, die aufgrund der geringen Dichte der Marsatmosphäre von untergeordneter Bedeutung sind12. Diese Gleichung wird für Ta über eine Wurzelfindungsmethode bei jedem Zeitschritt gelöst. Die Wärmeleitfähigkeit der Festkörper-Gewächshausschicht wird mit 0,01 W m-1 K-1 angenommen, was ein geeigneter Wert für die Wärmeleitfähigkeit von Silica-Aerogel bei Atmosphärendruck unter 0,1 bar ist (Ref. 17). Die Temperatur unmittelbar unter der Festkörper-Gewächshausschicht wird dann entsprechend der folgenden Kriterien entwickelt

Hier ist Fsol der tägliche mittlere Sonnenfluss an der Marsoberfläche (geliefert vom MCD) und μ¯(t,λ) der tägliche mittlere solare Zenitwinkel Cosinus, der vom Sonnenmodell zum Zeitpunkt t und Breitengrad λ ausgegeben wird. Schließlich, τ = αh ist die Festkörper-Treibhausschicht vertikale Pfad Extinktion optische Tiefe, wie in unserer vorherigen Analyse. Wir vernachlässigen konservativ den diffusen sichtbaren Fluss zur Schichtbasis aufgrund mehrerer Streueffekte.

Die anfängliche Oberflächentemperatur in unserer Simulation ist die jährliche mittlere Oberflächentemperatur an diesem Ort auf der Grundlage von MCD-Ergebnissen. Der anfängliche Regolith-Temperaturgradient wird auf die Mars-Geothermie eingestellt, die wir als 15 K km-1 auf der Grundlage eines angenommenen geothermischen Wärmeflusses von Fgeo = 30 mW m-2 und der mittleren Regolith-Leitfähigkeit von 2 W m-1 K-1 nehmen, wie folgt. 44. An der unteren Grenze gehen wir von einem festen Wärmestrom aus, der gleich Fgeo ist.

Wir gehen davon aus, dass der Regolith porös und mit Eis gesättigt ist, wobei das Eisvolumen-Mischungsverhältnis auf 0,5 eingestellt ist, was einer eisreichen mittleren Breitenregion wie Deuteronilus Mensae entspricht. Die Regolithdichte und die sensible Wärmekapazität wurden durch einen gewichteten Durchschnitt aus Basalt und Wassereis bestimmt. Wir fanden eine relativ geringe Empfindlichkeit unserer Ergebnisse gegenüber dem angenommenen Eis/Gesteinsverhältnis. Wir berücksichtigen die latente Wärme beim Gefrieren von Eis und beim Schmelzen von Wasser in der thermischen Berechnung, indem wir die Konzentration von Eis und Wasser auf jeder Ebene über die Zeit verfolgen, ähnlich wie bei Ref. 12. Wir zwingen dann die Temperatur auf oder unter 273.15 K zu bleiben, wenn Wärme in eine bestimmte Schicht eintritt und noch Eis vorhanden ist, und gehen davon aus, dass diese Wärme vollständig zum Schmelzen des Eises genutzt wird. Ähnliche Einschränkungen gelten für das Gefrieren von flüssigem Wasser unter Kühlbedingungen. Unser numerisches Modell wurde im Vergleich zu einer analytischen Lösung (Ausbreitung eines Gaußschen Impulses) validiert und verifiziert, um Energie und Gesamth2O-Masse weltweit zu sparen und die Präzision der Maschine bei jedem Zeitschritt zu gewährleisten.